Progression des cas importés, à qui la faute? (Par Pr Alassane Diédhiou)

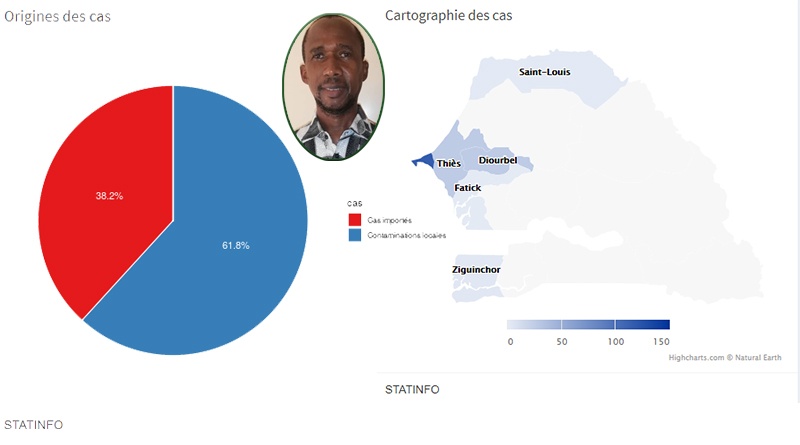
Ce mardi 31 mars 2020, le ministère de la santé nous a annoncé treize nouveaux cas, un peu moins que les vingt donnés la veille. Un fait attire notre attention, la progression des cas infectés est due au nombre élevé de cas importés et leurs contacts. Sur les 175 cas positifs, 74 sont importés, 91 contacts (contamination de premier degré) et 10 cas de contamination communautaire (On raisonne sur le nombre total sans tenir compte des cas guéris)..
Le gouvernement a accepté de recevoir nos compatriotes vivant à l’étranger, une chose normale, mais le problème est qu’il n’a pris aucune disposition de confinement de ces derniers. ce qui fait que certains parmi eux porteurs du
virus ont eu à infecter voisins ou parents. Cela se traduit par un nombre très élevé des cas cas de contact. Une maîtrise des cas importés (confinement ou auto confinement) permettrait d’inverser la courbe de progression des infectés.
Puisque les aéroports ont été fermés le 20 mars, nous osons espérer que le nombre de cas importés va drastiquement chuter, et par ricochet celui des cas de contact après le 4 avril 2020. Sinon, on pourrait conclure à un manque de
contrôle de nos frontières.
Dans les modèles mathématiques des épidémies les questions que l’on se posent sont les suivantes:
(1) Combien de personnes vont être infectées?
(2) Quand aura lieu le pic de l’épidémie?
Le paramètre le plus important (qui intéresse les épidémiologistes) est: R₀ = nombre moyen d’infections produites par un infecté, pendant la période où il est infectieux au début de l’épidémie. En effet,
• Si R₀ ≤ 1, il y a de très fortes chances que la maladie disparaisse au bout d’un certain temps
• Si R₀ >1, on a soit une épidémie mineure, soit une épidémie majeure.
Par exemple si R₀ = 2; un infectieux contamine au moins deux individus, ces derniers contaminent à leur tour chacun deux, ainsi de suite, et on se retrouve dans une progression exponentielle. Dans une épidémie majeure,
on considère τ la proportion de la population infectée. Cette proportion ne dépend que de R₀. Un calcul par ordinateur (ou calculatrice programmable) donne les valeurs approchées de τ en fonction de R₀:

On voit par exemple si R₀ = 2, on a 79% de la population qui pourront être infectés. D’où la nécessité de faire diminuer R₀ et le rendre inférieur à 1.
Comment obtenir la valeur R₀? Il y a plusieurs méthodes. Une parmi celles-ci, est de voir que:
R₀ = p × c × l.
• p= probabilité de transmission à un contact
• c= nombre de contacts par jour
• l= durée (nombre de jour) de l’infection.
Pour obtenir ces paramètres, il faut faire un suivi de tous les cas infectés. Les mesures de prévention visent à réduire R0 en réduisant;
• p: port de masques, lavage des mains
• c: confinement, éviter les transports en commun, les rassemblements
• l: diagnostic rapide, isolation des infectés (surtout les cas importés)
Pour le cas de la France, au 20 mars 2020, certains épidémiologistes ont estimé la valeur de R₀ = 2,5.
Pour le cas du Sénégal, cette valeur n’atteint pas la valeur 2 mais est vraisemblablement supérieure à 1. Le contrôle et le suivi des cas importés en plus des mesures de confinement pourraient aider à faire baisser R₀ et la ramener en dessous de 1.
Nota Bene: J’ai adopté une approche probabiliste, il y a aussi une approche déterministe.
Pour en savoir plus sur les modèles aléatoires, consulter les travaux de Tom Briton(Suède), Etienne Pardoux (Marseille) avec qui nous avions organiser une école sur les modèles probabilistes appliqués aux épidémies.
Prof. Alassane Diédhiou